Unsere Startseite zeigt eine Kármánsche Wirbelstraßenach dem ungarisch-amerikanischen Physiker von Kármán, 1881-1963. Dieses Phänomen ist in der Strömungsmechanik zu beobachten, wenn z.B. eine Platte mit einer Reynoldszahldimensionslose Kennzahl des Turbulenzgrades, nach dem britischen Physiker Reynolds, 1842-1912 um 100 umströmt wird. Hier entstehen wechselseitig ablösende Wirbel, die zu Druckschwankungen führen. Diese können so stark sein, dass sie (ohne entsprechende Gegenmaßnahmen) eine Brücke zum Einsturz bringen können. So ist es bei der Tacoma Brücke im Jahr 1940 passiert. Die Suchmaschine Ihres Vertrauens liefert interessante Videos.

Die Strömungsmechanikauch Fluiddynamik, Strömungslehre oder Strömungstechnik ist ein Teilgebiet der Physik und behandelt die Gesetzmäßigkeiten aller fließenden Stoffe, d.h. Flüssigkeiten und Gasezusammengefasst: Fluide. Die Luft, die uns umgibt, das Wasser der Meere, das Blut in unseren Körpern. Dies alles ist ohne Strömungsmechanik undenkbar. Aus diesen Beispielen wird deutlich, dass Körper im Allgemeinen umströmt (z.B. in der Aerodynamik) oder durchströmt (z.B. bei Rohren) werden.

Strömungsmaschinen wiederum bilden ein Teilgebiet der Strömungsmechanik. In diesen wird hydraulische LeistungP_hydr = Volumenstrom ∙ Druckdifferenz in mechanischeP_mech = Drehmoment ∙ Drehwinkelgeschwindigkeit umgewandelt und umgekehrt. Wird Fluiden Energie zugeführt (z.B. um Wasser durch einen Schlauch zu pumpen) spricht man von Arbeitsmaschinenz.B. Pumpen, Ventilatoren. Das obige Bild zeigt die Verdichterseite eines Turboladers, hier wird, wie vermutet werden kann, (Ansaug-)Luft verdichtet. Kraftmaschinenz.B. Turbinen, Windräder hingegen entziehen dem Fluid Energie (z.B. um in Kraftwerken mittels Generatoren Strom zu erzeugen). Die Güte der Energieumwandlung ist als Wirkungsgradη(griech.: eta) = P_hydr / P_mech (für Arbeitsmaschinen) definiert. Dieser wird üblicherweise in % angegeben und je höher dieser Wert ist, desto weniger Verluste treten in der Maschine auf.

Strömungsmechanik bzw. ‑maschinen finden Sie in allen Bereichen des täglichen Lebens. Dies können Sie nachfolgend anhand einiger Beispiele feststellen. Je nachdem welche / wie viele Aspekte Sie betrachten, gehen die Bereiche ineinander über, da Maschinen / Geräte normalerweise aus mehreren Bauteilen /-gruppen bestehen:

Somit kommen garantiert auch Sie täglich mit der Strömungsmechanik in Berührung. Und spätestens jetzt wissen Sie, dass Strömungsmechanik nichts mit (elektrischem) Strom zu tun hat, jedenfalls nicht direkt.

Nicht alles ist logisch

Technisch logische Überlegungen führen nicht immer zu strömungsmechanisch sinnvollen Lösungen. So kann es passieren, dass – trotz reiflicher Überlegung – Ihr gewünschter bzw. erwarteter Betriebspunkt in Ihrer Maschine / Anlage nicht erreicht wird. Eine mögliche Ursache könnte drallbehaftete Strömung sein, da das Fluid trotz gleicher Rohrlänge innerhalb des Rohres einen längeren Weg zurücklegen muss. Dies führt zu einem höheren Anlagenwiderstand / Druckverlust. Andere mögliche Ursache: In einer komplexen Anlage können die Verlustbeiwerteζ (griech.: zeta), z.B. für Automobile = Verlustbeiwert cW ∙ projizierte Fläche A der einzelnen Bauteile mitunter nicht einfach aufaddiert werden. Bauteile beeinflussen sich gegenseitigprinzipiell: je geringer die Entfernung, desto größer der Einfluss (nicht nur stromabwärts) und somit auch den Anlagenwiderstand. Mit unserer Erfahrung sind diese Herausforderungen – und alle weiteren – schnell und unkompliziert gemeistert.

Kontinuitätssatz / Massenerhaltung

Stellen Sie sich vor, wie gleiche Fahrzeuge in gleichen, konstanten Abständen durch einen Tunnel fahren. Gleiche Fahrzeuge besitzen gleiche Massen und auch Volumen. Gleiche Massen in konstanten Abständen kann auch als konstante Dichte interpretiert werden.

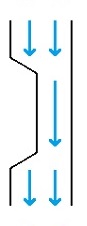
Der Kontinuitätssatz besagt, dass der Massenstrom(Fahrzeug)Massen pro Zeiteinheit ṁ = Q∙ρMassenstrom = Volumenstrom∙Dichte über ein Kontrollvolumen Z.B. besagter Tunnel konstant ist. Anders ausgedrückt: Die Masse, die hinein geht, kommt (zeitgleich) auch wieder heraus. Für unser Beispiel und für den Fall inkompressiblerWasser wird selbt in 4000 m Tiefe (d.h. 400  bar Druck) nur ca. 2 % komprimiert Fluide ist die Dichte konstant. Der Kontinuitätssatz vereinfacht sich somit hin zu konstantem Volumenstrom Q = v∙AVolumenstrom = (mittlere) Geschwindigkeit∙(Querschnitts)Fläche. Die Querschnittsfläche A wäre in unserem Beispiel gleich der Anzahl an Fahrspuren.

Stellen Sie sich weiter vor, der Tunnel wäre zweispurig und aufgrund einer Baustelle in der Mitte nur einspurig. In Fluidströmungen passiert nun etwas, das in der Verkehrswelt undenkbar ist. Statt beim Einfädeln abzubremsen (und dadurch einen Stau zu verursachen), beschleunigen die Fluidteilchen (analog der nebenstehenden Abbildung). Ihre Geschwindigkeit ändert sich umgekehrt proportional zum Querschnitt. In unserem Fall verdoppelt sich ihre Geschwindigkeit, da sich die Anzahl an Fahrspuren halbiert.

Satz von Bernoulli

Der Satz von BernoulliSchweizer Mathematiker / Physiker, 1700-1782 besagt, dass die Gesamtenergie eines Fluidteilchens entlang eines Stromfadensz. B. Fahrspur im Tunnel konstant ist. In Druck-SchreibweiseDurch Umstellen ist auch die Energie- und Höhen-Schreibweise möglich lautet dieser: p_tot = p_stat + p_dyn + p_geo = konstant. Der Totaldruck ist gleich der Summe aus statischem, dynamischem und geodätischem Druck und ändert sich entlang des Stromfadens nicht.

p_geo = ρ∙g∙HDichte∙(Erd)Beschleunigung∙Höhe ist primär von H abhängig und wird oft mittels der Wassersäule (WS1 mbar = 10 mmWS = 100 Pa) umschrieben. Es ist somit leicht verständlich, dass der Druck beim Tauchen steigtpro 10 m um ca. 1 bar oder dass Flugzeuge Druckkabinen benötigen, da der Druck mit der Höhe sinktpro 5.000 m auf ca. die Hälfte.

p_dyn = ρ / 2∙v² resultiert aus der Strömungsgeschwindigkeit und lässt sich leicht selbst erfahren, wenn man die eigene Hand anpustet oder diese beim Autofahren aus dem Fenster hält. In diesem Fall wird der dynamische Druck in eine Kraft umgewandelt, die Ihre Hand wegdrückt.

p_stat ist der Umgebungsdruck, auf der Erde − um uns herum − entspricht er dem Atmosphärendruck. Das sind immerhin ± 1.013 hPa = 101.300 Pa = 101.300 N / m² ≈ 10,3 Tonnen / m². Wir stehen somit − ohne dass jemand auf uns einwirkt − ganz schön unter Druck. Da der Druck in unseren Körpern jedoch gleich hoch ist, merken wir davon nichts. Veranschaulichen können Sie sich den statischen Druck, wenn Sie aus einer leeren PET-Flasche die Luft heraussaugen. Damit senken Sie den Druck im Inneren ab und sehen, wie die Flasche "von Zauberhand" durch den größeren Außendruck zusammengedrückt wird.

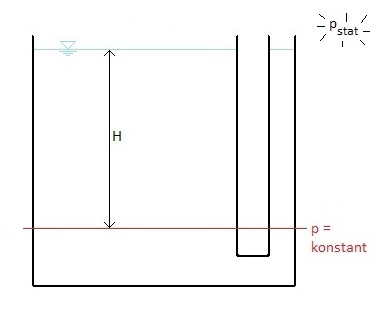
Bernoulli´s Satz zeigt auch anschaulich, dass der Druck nicht von der Fluidmenge abhängt. Dies ist als "Hydrostatisches Paradoxon" (siehe nebenstehende Abbildung) bekannt. Der Druck entlang der rot eingezeichneten Linie ist in diesem offenen Behälter konstant.

Impulssatz /-erhaltung

Schon NewtonEnglischer Universalgelehrter, 1643-1727 hat in seinem 1. Axiom festgehalten, dass sich ein kräftefreierVerluste, Reibung werden vernachlässigt Körper mit gleichbleibender Geschwindigkeit und Richtung fortbewegt. Die Geschwindigkeit kann hier auch null betragen, was einem ruhenden Körper entspricht. Somit ist I = m∙vImpuls = Masse∙Geschwindigkeit in einem kräftefreien Feld konstant. Es ist zu sehen, dass der Impuls über die Geschwindigkeit beeinflusst wird. Geschwindigkeitsänderungen (pro Zeiteinheit) werden durch Beschleunigen oder Bremsen (= negatives Beschleunigen) bewirkt.

Der Impuls ändert sich jedoch auch mit der Masse. Dies klingt zunächst paradox, da Massen normalerweise konstant sind. Das liegt an dem Umstand, dass wir dazu tendieren, die LagrangeItalienischer Mathematiker, 1736-1813 Betrachtungsweise zu nutzen. Diese ist objektbezogen, d.h. man ist ein mitbewegterWir sitzen im fahrenden Fahrzeug (= Masseteilchen) Beobachter. Im Gegenzug ist die EulerSchweizer Mathematiker, 1707-1783 Betrachtungsweise ortsbezogen, d.h. man ist ein außenstehenderWir stehen am Straßenrand und sehen Fahrzeuge vorbeifahren Beobachter. Impulsänderungen resultieren in einer Kraftwirkung auf den Körper. Daraus folgt das 2. Axiom und je nach Betrachtungsweise: F = m∙aKraft = Masse∙Beschleunigung bzw. ṁ∙v.

Einzelne Impulse von Körpern können sich im Sinne eines Gesamtsystems jedoch auch addieren oder aufteilen. Trifft beispielsweise eine Billardkugel auf eine ruhende zweite, bewegen sich beide Kugeln im Anschluss mit der halben GeschwindigkeitVerluste in Form von Reibung, Dämpfung usw. werden vernachlässigt der ersten weiter (da beide Kugeln gleich schwer sind).

Drehimpuls-/ Drallsatz

Der Impulssatz kann für den Fall der Bewegung auf einer gekrümmten Bahn mittels des Ortsvektors r (= Radius zum Drehzentrum) adaptiert werden. Daraus folgt der Drehimpulssatzauch Drall- oder Momentensatz: D = r x I = m∙(r x v) . Da nur der senkrecht auf dem Radius stehende Teil des Geschwindigkeitsvektors (= v_Uv_U = v∙cos α || uu = r∙ω = r∙2π∙n) zur "Hebelwirkung" beiträgt, lautet der Drehimpuls vereinfacht: D = m∙r∙v_U . Die zeitliche Ableitung des Drehimpulses entspricht dem Drehmoment: M = ṁ∙r∙v_U . Nach Einsetzen und Umstellen erhält man die Leistung: P = M∙ωMechanische Leistung = Drehmoment∙Drehwinkelgeschwindigkeit = ṁ∙Δ(u∙v_U) = Q∙ΔpHydraulische Leistung = Volumenstrom∙Druckdifferenz . Da hier eine ideale Maschine betrachtet wird, sind die Leistungen gleich groß, d.h. der Wirkungsgradη (griech.: eta) beträgt 100 %.

Laufräderauch Rotoren werden oftmals mithilfe sogenannter Geschwindigkeitsdreieckesiehe nebenstehende Bilder am Beipiel vorwärtsgekrümmter Schaufeln berechnet bzw. ausgelegt. Über v = u + w sind die Absolut- = Umfangs- + Relativgeschwindigkeit vektoriell verknüpft. α bezeichnet den Absolut- und β den Relativwinkel (= Schaufelwinkel). Die Indizes 1, 2 beziehen sich auf den Eintritt, Austritt des Schaufelkanals. Mittels der geometrischen Beziehung (Cosinus-Satzw² = u² + v² − 2∙u∙v∙cos α) und etwas Umstellen / Einsetzen lässt sich die Strömungsmaschinen-Hauptgleichung (SMHG) nach Euler herleiten: (u² + v² − w²) / 2 = u∙v_U . Der linke Term dieser Gleichung entspricht der zweiten Form und der rechte Term der ersten (üblicheren) Form der SMHG.

Integriert über das Laufrad ergibt sich: YSpezifische Schaufel- bzw. Stutzenarbeit = P / ṁ = u₂∙v_2u − u₁∙v_1u . Sie erkennen den direkten Zusammenhang zum abgeleiteten Drehimpulssatz. Falls die Zuströmung drallfreid.h. v_1U = 0 ist, wird Y (theoretisch) maximal. In realen Maschinen werden die integralen Größen (M, ω bzw. n, Q, Δp) gemessen und über den Quotienten beider LeistungenP_mech / P_hydr für Kraftmaschinen, P_hydr / P_mech für Arbeitsmaschinen der Wirkungsgrad ermittelt. Welche Strömungsmaschinen Bauart für den jeweiligen Anwendungsfall verwendet werden sollte (hoher Wirkungsgrad), kann mithilfe des CordierDeutscher Ingenieur Diagramms ermittelt werden.

Coriolis Kraft

Die CoriolisFranzösicher Mathematiker und Physiker, 1792-1843-Kraft gehört zu den Schein- bzw. Trägheitskräften und wirkt auf jeden Körper, der sich in einem rotierenden Bezugssystem bewegt. Diese Kraft lässt sich mittels des Foucaultschen Pendelsnach Léon Foucault, französicher Physiker, 1819-1868 veranschaulichen. Stellen Sie sich ein (entsprechend aufgehängtes) dicht über dem Boden schwingendes Pendel vor. Um das Pendel herum sind kreisförmig Plättchen aufgestellt. Es kann nun beobachtet werden, dass das Pendel scheinbar nicht nur hin und her schwingt. Das Pendel dreht sich bzw. wird abgelenkt, da es nach und nach die Plättchen umstößt. Tatsächlich ist es jedoch der Boden (die Erde mit uns als Beobachter darauf), der sich dreht.

Die Coriolis-Kraft kann analog zum 2. Newtonschen Axiom berechnet werden: F_C = m∙a_C = -2∙m∙(ω x v) . In dieser Gleichung entspricht ω der Drehwinkelgeschwindigkeit des Bezugsystems und v der Geschwindigkeit des sich darin bewegenden Objektes. Sie können die Coriolis-Kraft selbst erfahren, z.B. auf einer Drehscheibe (auf einem Spielplatz). Stellen Sie sich nach außen gerichtet auf die zu drehende Scheibe. Falls sich die Scheibe konstant dreht, können Sie ruhig stehen (angenommen, diese dreht nicht so schnell, dass Sie eine signifikante Fliehkraft erfahren). Machen Sie jetzt einen Schritt nach vorn, so werden Sie entgegen der Drehrichtung gedrückt, scheinbar ohne äußere Einwirkung.

Anlagen-/ Maschinenkennlinie

Die Leistungsfähigkeit von Strömungsmaschinen wird seitens der Hersteller oft in Kennlinien Diagrammen dargestellt. Das nebenstehende Beispiel zeigt die sogenannten Drosselkurven eines Trommelläufer Ventilators für drei Betriebsdrehzahlen (grau) und eine Widerstand-/ Anlagenkennlinie (grün). Ventilatoren bewegen i.d.R. Luft. Umgangssprachlich hört man oft die Begriffe Lüfter oder Gebläse, diese sollten im technischen Sprachgebrauch jedoch nicht verwendet werden. Korrekt heißt es Ventilator oder Verdichterbei Druckverhältnissen > 1,3. Falls kein Gas, sondern eine Flüssigkeit gefördert wird, spricht man von einer Pumpedie Luftpumpe ist eine berühmte Ausnahme.

Der Schnittpunkt aus Drosselkurve und Anlagenwiderstandentspricht i.d.R. einer quadratischen Funktion ergibt den tatsächlichen Betriebspunkt, hier BP1 bei 1000 U/min und BP2 bei 2000 U/min. Idealerweise sollte die Maschine bzw. generell der Maschinentypz.B. mittels des Cordier Diagramms so gewählt / ausgelegt werden, dass diese im gewünschten BP einen möglichst hohen Wirkungsgrad aufweist. Jedes Watt, das nicht verbraucht wird, muss an keiner anderen Stelle wieder eingespart und die Gesamtbetriebskostenengl. Total Cost of Ownership (TCO) können u.U. signifikant gesenkt werden.

Bei genauerer Betrachtung des Beispiels fällt Ihnen auf, dass sich mit Verdoppelung der Drehzahl n der Volumenstrom Q ebenfalls verdoppelt und der Druck p vervierfacht. Dieses Verhalten ist im Allgemeinen zu beobachten und lässt sich mittels der Affinitätsgesetze beschreiben: Q ∼ n∙D³, p ∼ n²∙D², P ∼ n³∙D⁵ . In diesem Beispiel verachtfacht sich somit die notwendige Leistung P, der Wirkungsgrad (nicht dargestellt) bleibt jedoch nahezu unverändert. Die Affinitätsgesetze können auch herangezogen werden, um die Leistungsfähigkeit unterschiedlicher Maschinengrößen (basierend auf dem Laufrad Außendurchmesser D) vorherzusagen. Bei doppelter Maschinengröße ändert sich Q achtfach, p vierfach und P 32-fach.

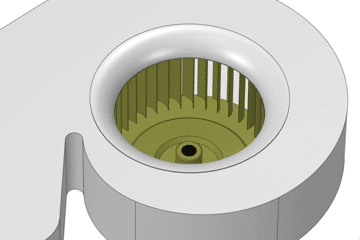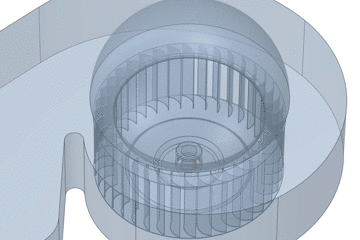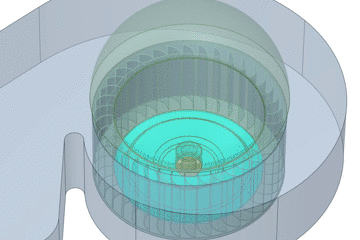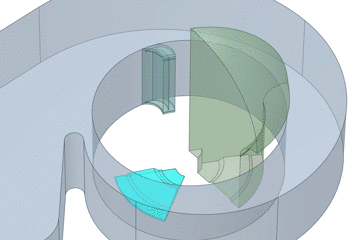
CAD-Modell → CFD-Modell

Um Strömungssimulationen durchführen zu können, ist es notwendig ein Fluidvolumen auf Basis des CAD-Modells abzuleiten. Für den Fall eines Ventilators, bei dem die Durchströmung relevant ist, werden alle „im Inneren liegenden“ Flächen zwischen Einlass und Auslass verwendet. Da im CAD-Modell keine Ein-/ Auslassflächen vorhanden sind, sind diese entsprechend zu modellieren (z.B. der Einlass mittels Hemisphäre). Kleine Spalte (z.B. um die Welle herum) müssen geschlossen werden, damit das Modell „dicht“ ist. Somit entsteht ein geschlossenes Volumen, das eigentliche CFD-Modell. Für das Beispiel des Ventilators, muss das CFD-Modell noch unterteiltin sogenannte Regionen bzw. Domänen werden, da dieses aus rotierenden und feststehenden Bereichen besteht. Für Parameterstudien, sehr große Modelle oder um Symmetrien auszunutzen, ist das CFD-Modell ebenfalls (sinnvoll) zu segmentieren. Dadurch sinkt unterm Strich der Zeitaufwand bzgl. der VernetzungRäumliche Diskretisierung. Durch entsprechende Sorgfalt an dieser Stelle können unnötige Kopfschmerzen im nachfolgenden Schritt vermieden werden.

Numerisches Gitter (Räumliche Diskretisierung)

Das numerische Gitter entsteht in dem das Fluidvolumen in viele kleine Kontrollvolumen (bis zu mehrere Millionen) unterteilt wird. Für jedes dieser Kontrollvolumen werden während der Berechnung die Massen-, Impuls- und (bei Bedarf) Energieerhaltungsgleichungen iterativ gelöst. Heutzutage werden numerische Gitter mittels Tetra-, Prismen-, Hexa-, oder Polyeder-Zellen generiert. Obwohl die (halb)automatischen Vernetzer in den letzten Jahren immer leistungsfähiger geworden sind, sind deren Ergebnisse immer (im Detail) kritisch zu betrachten. Nach wie vor sind es die Vorgaben / Einstellungen des erfahrenen Anwenders, die zu qualitativ hochwertigen Gittern führen. Die Gitterqualität kann mittels geeigneter Kontrollgrößen überprüft werden, z. B. Kantenlängenverhältnisseengl.: Aspect Ratio, Größenänderungenengl.: Volume Change von / zu oder (kleinste) Winkelengl.: Orthogonal Angle innerhalb der Zellen.

Um wandnahe Strömungen berechnen (und nicht nur modellieren) zu können, ist eine entsprechende, wandnahe Gitterauflösung notwendig. Die Güte dieser sogenannten Grenzschichtauflösung wird mittels des dimensionslosen Wandabstandes y+ beschrieben. In welcher Größenordnung sich der y+ Wert bewegen sollte, richtet sich nach der verwendeten Turbulenzmodellierung. Für die standardmäßig in der Industrie verwendeten SSTengl.: Shear Stress Transport- bzw. realizable-k-ε-Modelle sollte der Wert unter zwei liegen. Logischerweise ist für unterschiedliche Betriebspunkte (Strömungsgeschwindigkeiten) auch der y+ Wert (trotz identischem Gitter) verschieden. Die nebenstehende Abbildung zeigt den Schnitt durch ein typisches numerisches Gitter (Tetraeder inkl. Prismen-Grenzschicht, Laufraddurchmesser 90 mm).

Für Struktursimulationen wird „lediglich“ das eigentliche CAD-Modell vernetzt. Ein Punkt, weshalb der Aufwand gegenüber Strömungssimulationen deutlich geringer ist. Auch bedarf es hier keiner wandnahen Auflösung oder Turbulenzmodellierung.

Stationäre und transiente Berechnungen (Simulationen)

Für industrielle Anwendungen sollten (nach Möglichkeit) stets stationärezeitlich unabhängige Berechnungen genutzt werden. Hintergrund ist, dass transientezeitlich abhängige Berechnungen (im Schnitt) 20 malURANS vs. RANS länger dauern, ohne signifikante Mehrinformationen zu generieren. Für den Fall einer Pumpen oder Ventilator Berechnung ist es i. d. R. nicht relevant zu wissen, wie sich der Druckaufbau mit jeder Millisekunde ändert (siehe nebenstehende Animation). Wenn diese Maschine experimentell untersucht wird, erhalten Sie am Ende i. d. R. auch nur einen (mittleren) Wert für Druckaufbau, Antriebsleistung und Wirkungsgrad.

Bei stationär berechneten, rotierenden Maschinen werden die Schaufelkräfte mittels der Coriolis-Kräfte modelliert. Wenn die Schaufelanzahl hoch genugWie hoch hängt vom jeweiligen Fall ab ist, stellt dies auch kein Problem dar. Anders verhält es sich jedoch, wenn die Schaufelanzahl zu niedrig ist. Im Extremfall einer Abwasserpumpe mit nur einem SchaufelkanalDies minimiert das Verblockungsrisiko sind die Berechnungsergebnisse sehr stark von der Laufradposition abhängig. In solchen Fällen müssen Sie wohl transient berechnen. Oder Sie versuchen folgenden „Trick“: Sie berechnen mehrere Laufradpositionen stationär und mitteln diese Ergebnisse anschließend. Oftmals erhalten Sie dadurch die gewünschten Informationen und sparen im Vergleich zu transienten Berechnungen nach wie vor Zeit.

Transiente Berechnungen sind daher eher im Bereich der Forschung zu finden, wenn z. B. der Einfluss zeitlich begrenzter Phänomene untersucht werden soll. Hier werden auch deutlich aufwendigere Turbulenzmodellierungen (z. B. LESengl.: Large Eddy Simulation, DESengl.: Detached Eddy Simulation, DNSengl.: Direct Numerical Simulation) verwendet, was den Zeitbedarf nochmals deutlich erhöht. Instationäre EffekteInstabilitäten,
z. B. hohe Druckschwankungen bei stationären Berechnungen lassen sich bereits während der Berechnung auf Basis der Residuen und geeigneter Monitore feststellen. Falls (unerwünschte) instationäre Effekte bei Ihrem Produkt auftreten, sollte die Ursache hierfür ermittelt und z. B. mit einer Geometrieanpassung entgegengesteuert werden.

„Besondere“ Berechnungen

Bei „normalen“ Berechnungen ist das gesamte CFD-Modell mit lediglich einem Fluid (z.B. Luft oder Wasser) gefüllt. VOFengl.: Volume of Fluids Berechnungen ermöglichen die Verwendung mehrerer Fluide innerhalb eines CFD-Modells. So lässt sich z.B. das Einströmverhalten von Wasser in einen mit Luft gefüllten Raum berechnen (nebenstehendes Beispiel). Mittels VOF lässt sich ebenfalls das Verhalten von Festkörpernengl.: Solids innerhalb von Fluiden berechnen. Eine Anwendung wäre z.B. das Verhalten eines Schiffes auf dem Meer zu berechnen (zwei Fluide, ein Solid). Es versteht sich von selbst, dass VOF Berechnungen immer instationär sind.

Bei der FSIFluid Struktur Interaktion werden Strömungs- und Struktursimulationen gekoppelt und die Wechselwirkung zwischen Fluiden und Solids berechnet. Dies bedeutet, dass z.B. die aus der Strömung resultierenden Kräfte auf das FEMFinite Elemente Methode-Modell übertragen werden. Mittels dieser Kräfte wird die Spannungsverteilung innerhalb und die Verformung des Bauteils berechnet. Die berechnete Verformung (Geometrieänderung) wird in das CFD-Modell zurückgeführt und die Strömung darauf basierend neu berechnet.

Um die (vertraglich zugesicherten) Eigenschaften von Anlagen, Geräten, Maschinen usw. festzustellen, werden Messinstrumente, Prüfstände u.ä. verwendet. Bei Benutzung dieser Instrumente sind gewisse Aspekte zu berücksichtigen. Meist wird der Begriff Messunsicherheit als der wesentliche verwendet, wobei der Großteil der Anwender hier Wiederholbarkeit meint. Während bei neuen (kalibrierten) Messgeräten beide Begriffe sinngemäß das Gleiche bedeuten, ändert sich dies beispielsweise mit zunehmendem Alter / Gebrauch. Obwohl Sie immer identische Messungen durchführen, stellen Sie fest, dass sich Ihre Messergebnisse von den ursprünglichen Werten wegbewegen. Die Streuung der Messergebnisse (d.h. Wiederholbarkeit) bleibt zwar gleich, jedoch ist nun ein Offset vorhanden. Dies wird als Driften bezeichnet. Je nach Ausmaß muss das Messgerät dann rekalibriert werden oder Sie besitzen selbst das für Sie wesentliche Golden SampleGerät mit bekannten Eigenschaften o.ä. und können Ihr Messgerät damit justieren.

Die Messunsicherheit wird i.d.R. mit einem %-Wert angegeben, z.B. ± 1 %. Falls dieser Angabe kein weiterer Zusatz am Messgerät folgt, ist davon auszugehen, dass die Messunsicherheit auf den Skalen-Endwert bezogen ist (nicht Istwert). Dies führt dazu, dass Messungen von kleinen Größen in Relation zum Messbereich eine deutlich erhöhte Messunsicherheit aufweisen. Beispielsweise weist ein 100 A ± 1 % Strommessgerät bei einem Messtrom von 10 A bereits eine Messunsicherheit von 10 % auf. Relativ gesehen verzehnfacht sich die Messunsicherheit, wobei sie absolut gesehen konstant bleibt, hier ± 1 A. Sich dessen bewusst zu sein ist essentiell, um die Ergebnisse von verschiedenen Geräten an einem Prüfstand, einem Gerät an verschiedenen Prüfständen oder experimentellen vs. numerischen Ergebnissen beurteilen zu können. Auf der anderen Seite sollten Sie jedoch stutzig werden, falls Sie immer exakt das Gleiche messen.

In realen Maschinen werden normalerweise mehrere Messgrößen erfasst. Falls aus diesen Messgrößen weitere Kennwerte, Diagramme o.ä. abgeleitet werden sollen, ist die kombinierte Messunsicherheit k zu berücksichtigen. Nehmen Sie an, Sie ermitteln die Leistungsfähigkeit / Performance eines Ventilators. Die Messunsicherheit u bzgl. der Messung des Volumenstromes Q beträge 1 % und des Druckes p 0,5 % (jeweils vom Istwert). Die kombinierte Messunsicherheit beträgt somit k(Q,Δp) = √((u(Q))² + (u(Δp))²) ≈ 1,1 % . Falls Sie den Wirkungsgrad η bestimmen wollen, müssen Sie noch das Drehmoment M und die Drehzahl bzw. Drehwinkelgeschwindigkeit ω messen. Wir nehmen weiter an, die Messunsicherheit beträge jeweils 0,2 % für das Drehmoment und die Drehwinkelgeschwindigkeit (diesmal vom Endwert, d.h. 2 Nm bzw. 7000 U/min). Die kombinierte Messunsicherheit beträgt somit k(Q,η) = √((u(Q))² + (u(Δp))² + (u(M))² + (u(ω))²) ≈ 7,6...1,3 % . Die hydraulische Leistung lässt sich somit über den gesamten Betriebsbereich relativ genau bestimmen. Die mechanische Leistung (und somit auch der Wirkungsgrad) weist jedoch gerade zu kleinen Leistungen hin eine deutlich erhöhte Unsicherheit auf. Bei Messungen, die z.B. der Ermittlung eines Energie Effizienz Index (EEI) dienen, ist dies kritisch zu bewerten.

Es lohnt sich somit immer einen Blick ins Datenblatt zu werfen, bevor man Messtechnik anschafft bzw. nutzt. Es empfiehlt sich ebenfalls Ihre Auswertetools (z.B. Excel) kritsch zu betrachten und ggf. Formatierungsänderungen durchzuführen. Falls Sie Messgeräte mit einstelliger prozentualer Genauigkeit verwenden, ist es nicht sinnvoll mehr als zwei Nachkommastellen zu erfassen (auch wenn das Messgerät deutlich mehr ausgibt). Dies reduziert das sogenannte Augenpulver beim Betrachten der Ergebnisse und verbessert die Auswertbarkeit / Übersichtlichkeit deutlich.

Vorweg, bei Lean (d.h. „schlankes“) Management handelt es sich keineswegs um eine hochkomplexe Wissenschaft. Ganz im Gegenteil, im Prinzip genügen offene Augen, d.h. Wahrnehmung und Reflexion der Umwelt sowie stetige Hinterfragung. Der zentrale Inhalt des Lean Management ist die die Maximierung des Kundennutzens und Minimierung von Verschwendung. Der Pionier dieser Methode oder auch Philosophie, war Ōno Taiichijap. Ingenieur, 1912-1990, maßgeblicher Gestalter des Toyota Produktionssystems. Er entwickelte in diesem Zusammenhang die Basismethoden Kanbanjap.: Tafel oder Karte und Just-in-time Produktion. Das Kaizenjap.: „Wandel zum Besseren“ Konzept, auch als kontinuierliche Verbesserung bekannt, basiert ebenfalls auf seinen Ideen.

5 Lean Prinzipien

Werte

Der erste Grundgedanke ist, die Werte des Kunden in den Mittelpunkt zu stellen. Man versetzt sich in den Kunden hinein, um zu verstehen welche Wünsche besonders wichtig und welche weniger wichtig sind, z.B. mittels Bedarfsanalyse. Auf diese Weise ist es möglich die vorhandenen Ressourcen zielgerichtet einzusetzen. Es entsteht maximale Kundenzufriedenheit, da alle Erwartungen erfüllt werden. Gleichzeitig können alle Zusatzaufwände vermieden werden, die für das Erreichen dieser Zufriedenheit nicht relevant sind. Lückenlose Dokumentation und Kommunikation sind hier essenziell, z.B. mittels Lastenheft.

Wertstrom

Während der Wertstromanalyse werden alle notwendigen Schritte identifiziert, die für das Erreichen der Kundenzufriedenheit notwendig sind. Alle notwendigen Schritte bzw. Prozesse und deren Reihenfolge sowie Verantwortlichkeiten werden erfasst, z.B. mittels Pflichtenheft. Es existieren drei verschiedene Prozessarten: wertschöpfende, wertermöglichende und unnötige. Erstere sind zu priorisieren, da diese direkt die Kundenzufriedenheit beeinflussen. Zweitere sind notwendige, um z.B. langfristige Qualität sicher zu stellen. Letztere sind generell zu vermeiden.

Fluss

Der Wertstrom soll möglichst verlustarm durch alle Prozesse und Projektphasen fließen. Idealerweise sind bereits während der Wertstromanalyse Maßnahmen getroffen worden, damit der Wertstrom nirgends gehindert, aufgestaut oder überlastet wird. Hierzu gehört beispielsweise das Ermitteln von Abhängigkeiten oder das Ableiten von Alternativplänen im Fehlerfall. Durch immer wiederkehrende Reflexion möglicher Verschwendung – siehe unten – werden diese Maßnahmen fortlaufend effizienter.

Pull

Das Pull-Prinzip fokussiert die Bedürfnisse des Kunden. Es wird beispielsweise nur das produziert, was der Kunde benötigt und auch erst dann, wenn er es benötigt. Auf diese Weise wird die Nachfrage bedient, der Projektablauf orientiert sich am Kunden. Werden eigene Vorgaben und Ziele priorisiert oder dem Kunden aufgedrängt, spricht man vom Push-Prinzip.

Perfektion

Die ersten vier Lean-Prinzipien müssen immer wieder durchdacht und neu bewertet werden. Mittels immerwährender Selbstreflexion, Berücksichtigung neuer Ansichten und Erkenntnisse wird der Fluss stetig optimiert. Dieser Vorgang wird durch Kaizen ausgedrückt und endet nie.

7 + 2 Möglichkeiten Verschwendung zu reduzieren

• T – Transport → Transportwege
• I – Inventory → Lagerhaltung
• M – Movement → Bewegungen
• W – Waiting → Wartezeiten
• O – Overproduction → Überproduktion
• O – Overengineering → Unnützes
• D – Defects → Mängel

Durch Beobachtung und Analyse identifizierte Ōno drei Haupthindernisse, die effiziente Prozesse beeinträchtigen: Murajap.: Unregelmäßigkeiten, Murijap.: Überforderung und Mudajap.: Verschwendung. Hieraus leitete er sieben Muda Kategorien ab, die sich mittels des Akronyms TIM WOOD zusammenfassen bzw. merken lassen.

Im Laufe der Zeit kamen noch zwei Arten hinzu: Mitarbeiterpotenzial (Employee potential) und Kommunikation (Communication). Wird von Ressourcen gesprochen, sind Menschen, Maschinen und (Roh-) Materialien gemeint. Das sind drei der ursprünglichen vier M (Mensch, Maschine, Material, Methode) laut Ishikawa Kaorujap. Chemiker, 1915-1989, Erfinder des nach ihm benannten Fischgräte-Diagramms. Dieses stellt Ursachen und Wirkungen bzw. mögliche Fehlerursachen dar und ist eines der sieben elementaren Qualitätsmanagement Tools (Q7 – Strichliste, Histogramm, Pareto-Diagramm, Ishikawa-Diagramm, Streudiagramm, Qualitätsregelkarte, Ablaufdiagramm).

Transport

Ressourcen müssen von A nach B transportiert werden. Jeder Transport kostet Geld und birgt die Gefahr von Schäden, Unfällen sowie Zeitverzug. Unnötiger oder verzögerter Transport verursacht Wartezeiten, wenn eines der „Rädchen“ nicht zur richtigen Zeit am richtigen Ort ist. Mitarbeitende können nicht produzieren wenn Material fehlt und andersherum. Vorausschauende Planung und Steuerung (Just-in-time) sowie Kanban sind hier nützliche Mittel. Gute Einkäufer berücksichtigen bei der Beschaffung die Transportkosten und -zeiten und nicht nur den reinen Teilepreis. Dies kann genannten Risiken reduziert und die lokale Industrie stärken.

Inventory

Überschüssige, nicht unmittelbar nutzbare Ressourcen beanspruchen Platz und binden Kapital. Vorhaltung von Lagerflächen kostet Geld, für alle Arten von Ressourcen. Nicht Verarbeitbares oder Veräußerbares schränkt die Liquidität ein. Es besteht die Gefahr von Schäden, da die Dinge „im Weg herum stehen“ oder evtl. abhanden kommen. Mittels ABC-Analyse können Ressourcen nach Wertschöpfungsrelevanz klassifiziert werden. A-Ressourcen sollten besonders überwacht und vorgehalten werden, da diese für den Geschäftsbetrieb essenziell sind. B-Ressourcen haben eine mittlere Wertschöpfungsrelevanz. C-Ressourcen sind oftmals Verbrauchsmaterialien, die in Massen vorhanden und schnell beschaffbar bzw. austauschbar sind. Auch hier kann mittels Just-in-time, Kanban und enger Zusammenarbeit mit Lieferanten und Abnehmern die Lagerfläche auf das tatsächlich notwendige Maß reduziert werden.

Movement

Unnötige Arbeitsschritte sowie Bewegungen sind ineffizient. Hierzu gehören ungünstige Platzierungen von Einzelteilen, Werkzeugen sowie nicht ergonomische Arbeitsplätze und -positionen. Dies verlängert die Bearbeitungszeit, reduziert die Produktivität und birgt ggf. die Gefahr von Qualitätsproblemen sowie Verletzungen. Laufwege quer durch das Lager oder Gebäude und das Ausfüllen von unnützen Checklisten sind weitere Aspekte. Letztere sind z.B. unnütz, falls sie im weiteren Prozess (auch bei der Dokumentation) keine Rolle spielen, da die Daten nicht ausgewertet werden oder diese nicht eindeutig zuzuordnen bzw. nachzuverfolgen sind. Das Einrichten von standardisierten, ergonomischen Arbeitsplätzen, sowie das „Lehren und Leben“ nach der 5S-Methode schaffen hier Abhilfe. 5S steht für Sortieren, Systematisieren, Säubern, Standardisieren und Selbstdisziplin.

Waiting

Zeiträume, in denen Menschen oder Maschinen nicht produktiv sind und auch keine Produktivität ermöglichen, sind zu vermeiden. Diese entstehen, wenn auf Informationen, Ressourcen oder Fertigstellung vorangehender Arbeitsschritte gewartet wird. Auch hier kann mittels ABC-Analyse festgestellt werden, welches die „kritischen Rädchen“ sind, damit nicht aus kleinen Ursachen, große (negative) Wirkungen resultieren. Produktivität wird beispielsweise durch präventive Wartung, kurze Wege und eindeutige, rechtzeitige Kommunikation ermöglicht und verbessert.

Overproduction

Wird mehr produziert, als tatsächlich notwendig oder bestellt worden ist, ist das i.d.R. Verschwendung. Dieser Bereich sollte sehr gründlich analysiert werden, da hierdurch viele weitere Bereiche beeinflusst werden: Transporte, Lagerflächen, Kapitalbindung, Bewegungen, Beschädigungsgefahr. Jedoch ist ein gewisses Auf-Lager-Produzieren sinnvoll, um Störungen ausgleichen sowie flexibel und schnell reagieren zu können. Durch mit Lieferanten und Abnehmern abgestimmter Bedarfsplanung und Losgrößen, kann hier die goldene Mitte gefunden werden.

Overengineering

Ressourcen sollten nicht eingesetzt, um Eigenschaften oder Funktionen umzusetzen oder Materialien einzusetzen, die vom Kunden weder gewünscht noch bezahlt werden. Dies schmälert die Profitabilität. Alles, was keinen Mehrwert bietet und die Komplexität unnötig erhöht, sollte weg gelassen werden. Dies ist ebenfalls die große Kunst des Konstruierens. Es ist ggf. jedoch der eigene Qualitätsanspruch zu berücksichtigen. Nur weil der Kunde evtl. eine „billige Lösung“ will, muss man diesen Weg nicht zwangsläufig mitgehen, denn am Ende fällt dies bei Ausfällen und Defekten auf einen zurück. In solchen Fällen sollte mit logischen und nachvollziehbaren Argumenten Überzeugungsarbeit geleistet werden. Es kann jedoch auch notwendig sein, z.B. im regulierten Umfeld, mittels höherer Komplexität Redundanzen zu schaffen oder Materialien mit höherer Haltbarkeit zu verwenden und somit die Ausfallsicherheit zu maximieren.

Defects

Fehler und Qualitätsmängel oder auch fehlende Funktionen im Prozess bzw. Produkt sind zu vermeiden. Diese führen zu Nacharbeit und Verzögerung und verursachen somit Kosten sowie ggf. auch die Schädigung des eigenen Ansehens. Je später diese Unzulänglichkeiten in der Entwicklung oder Fertigung auffallen, desto teurer wird es. Dies lässt sich mittels der sogenannten Zehner-Regel anhand eines beispielhaften Prozesses veranschaulichen. Chronologisch eingeteilt in 1. Analyse, 2. Konzeption, 3. Entwicklung, 4. Testing, 5. Produktion, 6. Kunde. Pro Abschnitt verteuern sich unentdeckte Fehler um Faktor Zehn. Während Fehler, die im Zuge der Analyse entdeckt werden symbolisch einen Euro kosten, kosten dieselben Fehler, falls erst beim Kunden auffallend, bereits 100.000 Euro. Eindeutige und klare Kommunikation, sowie lückenlose Dokumentation der Pflichten- und Lastenhefte inkl. Verantwortlichkeiten sind hier das erste Mittel der Wahl. Die Berücksichtigung Ishikawa`s Q7 kann an dieser Stelle Kopfschmerzen ersparen.

Employee potential

Ungenutztes Wissen, Kreativität und Fähigkeiten, d.h. Kompetenzen eigener Mitarbeitenden sind hier gemeint. Durch ungeeignete Position-Zuordnung innerhalb des Teams oder Produktentstehungsprozesses, geht Mitarbeiterpotenzial verloren und führt zu Demotivation, sinkender Produktivität oder Mängeln. Das Mitteilen eigener Wünsche und Vorstellungen sowie aktiver Austausch zwischen Mitarbeitenden und deren Führungskräften ist essenziell. Keine Partei sollte auf die andere warten, sondern jeder proaktiv agieren. Hierdurch können auch ungeahnte Potenziale aufgedeckt werden, da z.B. nicht alle Informationen über einen Menschen in seinem CV stehen (müssen).

Communication

Dieser Punkt befasst sich maßgeblich mit der Flut an Mails die tagtäglich empfangen – und somit auch versendet – werden, unproduktiven Meetings sowie unnötigen Nachfragen. Klare Kommunikationsregeln, wer was wann wissen muß, helfen hierbei. Es ist nicht förderlich jeden Kollegen in CC zu nehmen, damit dieser „Bescheid weiß“. Die Annahme, das dem so sei ist schlicht falsch, denn (zu viele) Mails gehen schlicht unter. Wenn ein Meeting anberaumt wird, sollte sich der Initiator im Klaren sein, was das Meeting zum Ergebnis haben soll. Hierzu ist das Erstellen einer entsprechenden Agenda unabdingbar, denn so werden Inhalte – somit auch notwendige Teilnehmer – definiert und die Eingeladenen können sich im Vorfeld vorbereiten. Unnötige Nachfragen werden vermieden, wenn das eigene Tun und Handeln im Gesamtprozess reflektiert wird. Was einen Kollegen fünf Minuten kostet, kann im weiteren Verlauf durchaus eine Stunde oder mehr einsparen. Proaktiver Austausch sensibilisiert alle Beteiligten bzgl. Ihrer Bedürfnisse. Dass die eigene Sprache so genutzt wird, wie sie (offiziell) definiert ist, sollte selbstredend sein, z.B. ist Leistung nicht das Gleiche wie Energie.

Nützliche Verschwendung

Auf der Suche nach Verschwendung ist es wichtig zwischen nützlicher und nicht nützlicher zu unterscheiden. Neben wertschöpfenden Prozessen existieren auch wertermöglichende, d.h. diese haben zunächst keinen direkten Anteil an der Wertschöpfung. Ein Beispiel für wertermöglichende Prozesse sind (Langzeit-) Testläufe. Testläufe sind für die langfristige Sicherstellung der Qualität und somit Kundenzufriedenheit essenziell. Es ist besondere Vorsicht geboten, falls im Rahmen von Einsparungen eben an dieser Stelle der Rotstift angesetzt werden soll. Ein anders Beispiel ist die „ungeliebte“ Dokumentation. Diese biete ebenfalls keinen direkten Mehrwert, sorgt jedoch für Klarheit und somit bessere Kommunikation sowie Rechtssicherheit. Rechtssicherheit ist ein nicht zu unterschätzender Faktor, denn gerade im regulierten Umfeld ist es notwendig nachzuweisen, dass alle zu berücksichtigenden Vorschriften eingehalten worden sind. Jedoch gilt hier – wie im gesamten Leben – alles mit „zu“ ist nicht gut, zu viel aber auch zu wenig.